Highly Strung? A Possible Solution
By Ad van Beers
Timothy Garcia sat there alone on the huge stage of the Hong Kong Island concert hall and retuned his guitar for the umpteenth time, and as I fought with the impulse to stand up and offer some assistance, the apologetically smiling guitar player proceeded to put his guitar systematically out of tune before each piece of his (mostly Villa Lobos) program.
Share this:
[feather_share]
Then he would commence playing and with a deftness indicating considerable experience, his left hand would take lightning fast trips from fingerboard to tuning pegs and with his ears and his memory of the music as a guide he would finally tune his guitar whilst playing -with varying degrees of accuracy.
The problem was, and as far as I know still is, he did not seem to know about tempered fifths. After tuning A (fifth string) with the aid of a tuning fork to A 110 Hz*, he would tune E (first string) by taking a seventh fret harmonic on A; thus E (first string) would end up 330 instead of the correct 329.6. Two or three steps further on, still using seventh fret harmonics, the poor guitar would be totally out of tune.
A similar result can be obtained by playing a chord whilst tuning. Our ears will insist on the most harmonious sound, the chord will sound nice but the guitar will be out of tune.
The tempered** fifth is the means by which modulation is possible.
To understand harmony, it is essential to understand timbre and our human way of evaluating sounds.
The reason for the guitar to exist is timbre control coupled with polyphony. That is its niche in the realm of musical instruments. Timbre, also known as sound texture or sound colour, is the result of a particular mixture of frequency components. Each sound produced on a string is in fact a mixture of possible frequencies determined by idiosyncratic and imposed conditions.
Idiosyncratic determinants are: Length, Mass and Tension of the string and the structural tensions in the guitar body. Imposed conditions are: point of impact along the string length and the shape and direction of the striking.
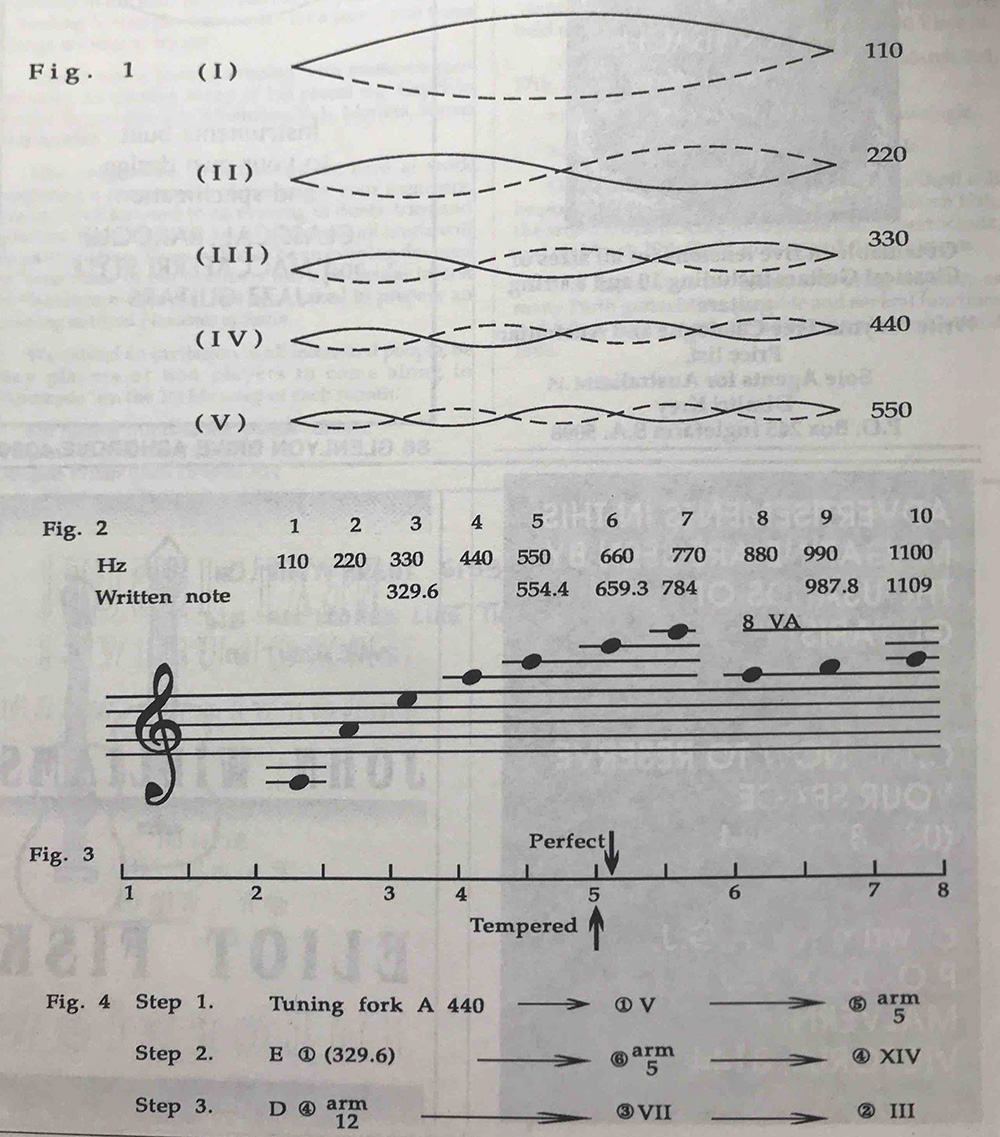
Some of the possible frequencies of A (fifth string) are shown in Fig. 1.
Pitches corresponding to the first ten modes of vibration are shown in Fig. 2 (1 have included the true frequencies of the written notes. These discrepancies give a clue to the unpleasant harshness of sounds rich in high partials).
Our brain, via the ears, recognises the mixture of frequency components or partials and we are aware of it as colour or texture. Many high partials result in bright, thin sound and predominantly low partials result in warm, rich, mellow sound.
It is important to note the absence of calibration*** and the general vagueness of our sense of timbre perception. The same applies to our evaluation of modern harmony (except the ultimate in harmonic beauty – UNISON or sameness. With a little practice anyone can learn to positively identify the sameness of two strings in unison).
Why is the octave such a satisfying harmonic relationship? Answer: Because of the 2:1 ratio of the sound frequencies. Similarly, the fifth is at its most perfect when the ratio is 3:2. We might call it the Pythagoran**** fifth. The annoying thing about it is its asymmetrical placement in a scale. Eighteenth Century com- posers and theorists wishing to create ever larger musical structures, agreed to lower the fifth in the scale (see Fig. 3) in order to create symmetry and the possibility of modulation.
The interval of the fifth is therefore no longer pure, the frequency no longer 150% of the tonic but 149.64%. Thus A (fifth string) 110 = E (fourth string) 164.8, and E (sixth string) 84.2, E (first string) 329.6.
The placement of the frets is such that when we play (fifth string) on the seventh fret, we produce 164.8 and on the nineteenth, 329.6. However, if we play the fifth string seventh fret harmonic, we can only get 330 (110 x 3), the untempered Pythagorean beautiful, perfect fifth, which sounds lovely but is useless as a tuning aid.
CONCLUSIONS
• Given that fifths are not what they used to be and harmonic purity is no longer attainable on our modern instruments,
• Given the imprecision of our ability to accurately perceive these new harmonic relationships, we must avoid listening to harmony whilst tuning.
Two more factors pertaining to tuning are worth mentioning here:
1. Human ears are most efficient between 300 and 2000 Hz.
2. The guitar is idiosyncratically biased to produce A 110 and its heavy relatives, E B and D, thus my preferred system of tuning is (see Fig. 4).
Explanation of Fig. 4.
Step 1. Listen to tuning fork. Adjust (first string) played at fifth fret and (fifth string) by playing a fifth fret harmonic.
Step 2. Listen to open E (first string); adjust (sixth string) by playing fifth fret harmonic; and (sixth string) played at fourteenth fret.
Step 3. Listen to (fourth string) by playing a twelfth fret harmonic, and adjust (third string) played at seventh fret, (second string) played at third fret.
* Hz – Hertz, a frequency of one cycle per second.
** Adjustment made to the pitch of a note.
*** The determination of accuracy.
**** Of Pythagoras, a Greek philosopher and mathematician.